When my friends and I first played an escape room in 2013, we were impressed by its novelty and had the time of our lives. However, after having played many more escape rooms, I also saw design patterns emerge. Escape rooms are information systems in the form of rooms, operating under similar rules to produce a unique genre of puzzle-solving experiences. As Sawyer Kemp points out, escape rooms seduce players with an “escape from social constraints.” Escape rooms also integrate various fun aspects from other entertainment media. Scott Nicholson suggests that escape rooms can be viewed as a medium of convergence with several precursors, including live-action role-playing (larp), point-and-click adventures, puzzle and treasure hunts, interactive theater and haunted houses, adventure game shows, and themed entertainment.
This prior work on escape rooms discussed the history and appeal of escape rooms. Here, however, I contend that escape room games can be viewed as a platform of analog computing. By way of this platform, escape rooms are created, adapted, deployed and played. My central question is: How does computing take place in this platform? A corollary question is: How do the players’ and designers’ experiences of escape room computation differ?
Under the Platform Studies Platform
Platform Studies, a subfield of digital media scholarship focused on the computational and cultural relationship between hardware and software, has primarily considered gaming consoles and other devices as digital platforms. Nick Montfort and Ian Bogost’s work on the Atari VCS console in 2009 became the first in the MIT Press book series Platform Studies. It focuses on the technological aspects of the console, from the computational power of the chips, to the syntax of the software code, to the performance details of displaying graphical content on the screen. Later works in the book series, such as Codename Revolution, I Am Error, and Now the Chips Are Down, have expanded the notion of platform beyond the consoles themselves, taking user documentation, the culture and context, the lesser-known history, and the social interactions among players into account.
While the Platform Studies series has established the canonical media-archaeological approach to studying digital platforms, we cannot take precisely the same methodological approach to study escape rooms as platforms, considering that the technological component of the escape room platform is fundamentally different than that of digital platforms. For one thing, escape rooms are analog games. Although they typically involve digital systems, their main gameplay consists of interacting with physical artifacts in a materialized game scene. Digital systems used in escape rooms, such as a Raspberry Pi for playing videos or customized circuit for triggering switches, have already reached a level of complexity and diversity that makes the media-archaeological approach in traditional platform studies hardly applicable. There is no such single circuit board that every escape room designer chooses to use in their games. Even though one can survey all the digital systems in the history of escape rooms, the digital systems are not the core technological platforms running the gameplay. Nevertheless, the whole escape room functions itself as a platform for computation.
According to Nick Montfort and Ian Bogost, the study of (digital) gaming platforms involves five layers as shown in the following diagram, where the platform layer at the bottom can affect the layers above it.
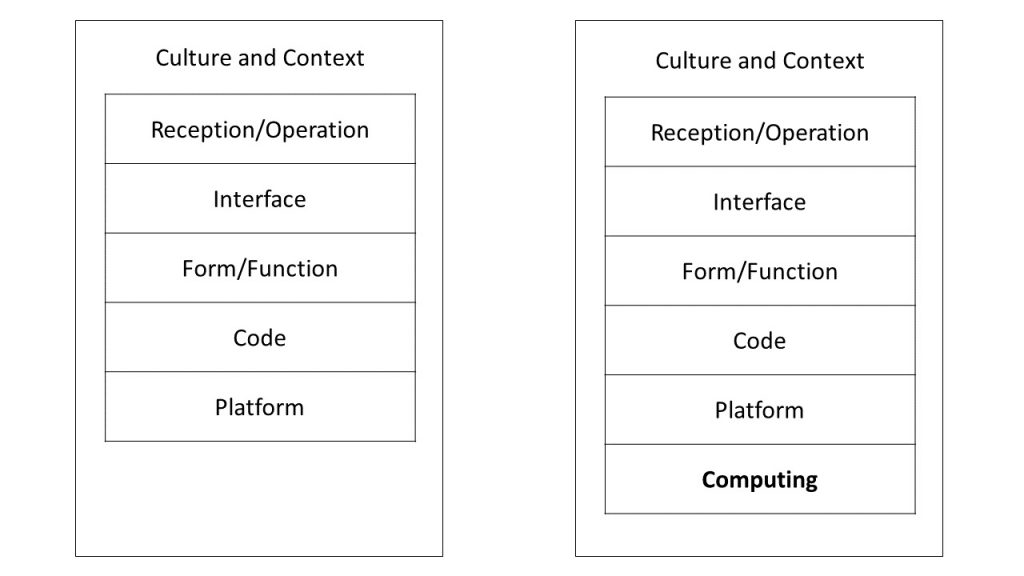
Figure 1. Left: The five levels of digital media, situated in context, from Nick Montfort and Ian Bogost’s foundational work of platform studies. Right: This study adds another level under the Platform level to related to the basics of non-electronic computing.
For digital game platforms, the platform layer usually consists of specific hardware, devices powered by chips and circuits. These components generate computational states. When we discuss the platform of digital media, we rarely need to dig further into how the chips and circuits function to generate computation, because this complicated process has been standardized and made into modules. Their computational behaviors are abstracted by numbers on the “technical specs” of the product.
When it comes to analog game platforms, however, there are no such standardized computing components as chips and circuits. We have to turn our attention to the non-digital components, such as the physical space, the artifacts, and even the human actors in the game, examining how they operate under the rules of the game to create computational states. In other words, platform studies for analog games demands additional analysis on how an analog game platform is computational.
Analog Games as Computers
Card games were the main entry point for analog game scholars doing such platform analysis. Nathan Altice’s “The Playing Card Platform” examines how five characteristics of cards – (1) planar, (2) uniform, (3) ordinal, (4) spatial, and (5) textural – support the generation of bits. For example, cards being planar means they can switch between facing up or facing down to represent 1-bit information. Based on Altice’s work, Jan Švelch discusses how the cards of Magic: The Gathering (1993) inherit these characteristics but are also further affected by community practices such as the manufacturing process and the secondary market.
In contrast to this emphasis on the materiality of cards, Ian Bellomy proposes that people are, in fact, the source of computing for analog game platforms. It is the people rather than the materials that do the computation by assigning significance to the physical attributes. Bellomy radically challenges the view that the materials solely define a platform and points out that even the output values of electric transistors inside digital platforms need to be further encoded by people in order to make computational sense.
I acknowledge the subjectivity of people in performing the act of computing. However, I disagree when Bellomy suggests that “platform studies has nothing to say about analog games” just because all the computation is performed by people or because the materiality of the game does not compute. If this is true, we can say that digital platforms with billions of transistors also do not compute because it is the people who build them all and decide the rules they operate. In fact, even Bellomy acknowledges the distinct differences between the number of transistors in digital systems and the number of artifacts in analog games. But he suggests that the function of people in the computation is more salient in analog games than in digital machines.
On this point, I support Altice and Švelch in emphasizing the importance of materiality in computing for platform studies of analog games. Ultimately, without the materials present, we cannot realize that computation is taking place. Platform studies neither begins nor ends with the subject who performs the computing, nor is it about pancomputationalism, i.e., the idea that everything is computational. A platform involves not only people who perform the computing, but also the materials that we intentionally make to enable and facilitate the computing. It is arbitrary to study people as the only computing platform, or to trend the discussion on the materiality towards pancomputationalism to diminish its importance to the platform. Platform studies for analog games should avoid these two extremes. Material components in escape rooms are salient, too, in the process of computing. The peculiarities of the material components and their complex interactions in analog game platforms, such as in escape rooms, are worth serious academic study, especially in light of the already standardized electrical components in digital platforms.
Analog games are rule-based systems. According to a mechanistic account on computation proposed by Gualtiero Piccinini, a physical computing system is, by design, mechanisms that manipulate a medium-independent vehicle according to rules, which provide mappings among inputs, outputs, and internal states of the system. By medium-independence, it means that human brains, circuits, and material artifacts in analog games can all be considered as the medium where physical computation takes place.
Therefore, the interaction of objects and minds according to the rules of an analog game is a form of computing. We are so used to how computing runs seamlessly under digital systems that we fail to acknowledge the many forms of analog computing that accompany them. The playing card platform is the tip of an iceberg. It is time that we embrace analog games as a database of analog computers. Analog games show how computing can be enabled and facilitated not only by voltages, chips and quantum mechanics, but also by tokens, objects, and minds.
Analog Components of Digital Computing
To understand analog computing in escape rooms, let us first review how the digital computing of modern computers is generated by physical components.
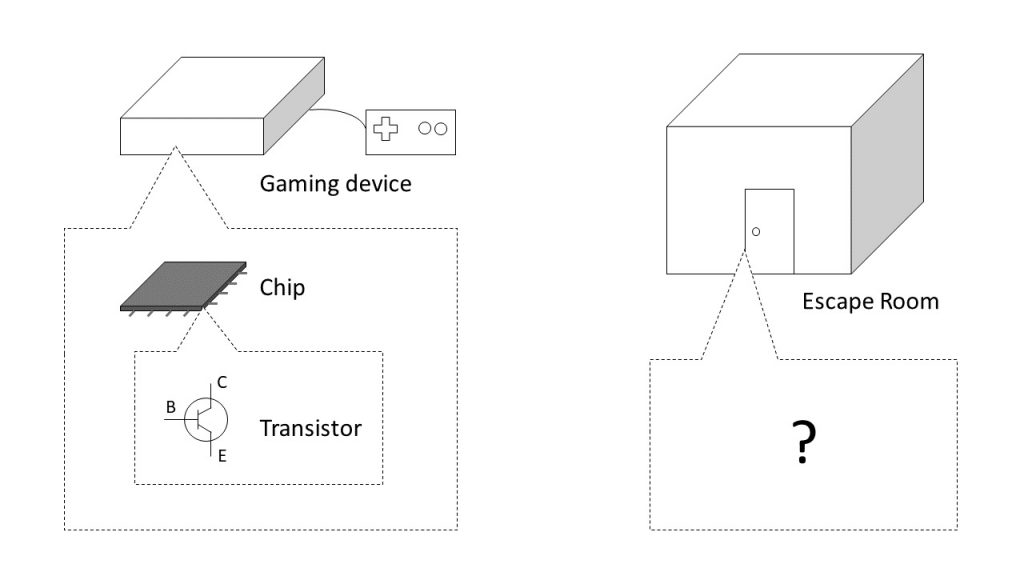
Figure 2. The mechanism that generates computing in digital gaming devices is often ignored in platform studies, because the ways that transistors and chips work to form a computer are too complicated and have already been standardized. However, how computing is done in analog game systems like escape rooms is underexplored.
When authors of platform studies discuss digital gaming platforms, their lowest unit of analysis inside the digital platforms is usually the chip. Inside a chip, there are many electric components integrated in a tiny area. One kind of component that generates the basic logic state of 1 and 0 for computing is the transistor. As shown in Figure 2, a transistor has three ports, and the port in the middle (B) is used to control the logic state reflected by the other two ports (C and E). Basically, if there is an electric current flowing into B, then C and E will be conductive to allow electric currents to flow through CE, creating a logic state of 1. Otherwise, there will not be any electric current flowing through CE, and the logic state will be 0. Although the chips are the crystallization of components including transistors that generate the basics of 1s and 0s, they were not built to be salient and interactive to players. Researchers only need to trace the performances of the chips used in the platform to discuss the hardware of the platform in numbers and to draw their relationship to the expressive content that the platform presents. The materiality of the transistors can be ignored. An escape room is a room-scale device that can function with components other than chips to generate computational logics. When we view it as a platform, we can explore its components and understand how they interact with each other.
One-Bit Components in Escape Rooms
Perhaps the most obvious component that generates two states in the platform is the door. The door controls access to a room. It is usually installed with an electric switch that controls the opening and closing of the door. When the door is open, players get to explore everything in a new space that was not available to them when the door was previously closed. This one bit of information can bear various meanings depending on where it is in the game: entering the first room, unlocking a new scene, winning the game, and so forth. The material property of the door having a solid, non-transparent body makes it an ideal analogy device to create the one-bit logic by dividing spaces into separate game scenes.
Another one-bit component is a key-lock puzzle consisting of a lock and the right key to open the lock. The key may be found by searching the room or more often, gained as a reward of solving another puzzle. Conceptually, the key-lock puzzle is similar to the door in that it preserves the access to a specific space, such as what is inside a box or a cabinet. Opening the lock usually means gaining new clues to other puzzles in the room.
Note that the one-bit update of opening the key-lock puzzle is just an example of solving any puzzle in general. Each puzzle in the game system can be modeled with a one-bit processor with the two states of “solved” and “unsolved.” The entire gameplay can be viewed as a path to solve a series of puzzles, a path where players need to turn all the puzzles from the “unsolved (0)” state to the “solved (1)” state.
This puzzle machine model quite resembles a Turing Machine, which had informed the building of digital computers. Invented by Alan Turning, who is considered as the father of modern computer science, Turing Machine is an abstract computing model operating under prescribed instructions. It consists of (1) an infinite tape divided into adjacent cells, each of which can store a symbol on it, (2) a head that can traverse the cells to read and write symbols, (3) a state register that stores the state of the machine, (4) instructions for the machine to update to new states given its current states by updating the symbol on the current cell and moving to another cell (or doing nothing). The following diagram shows the process of solving a series of puzzles using the Turing Machine model:
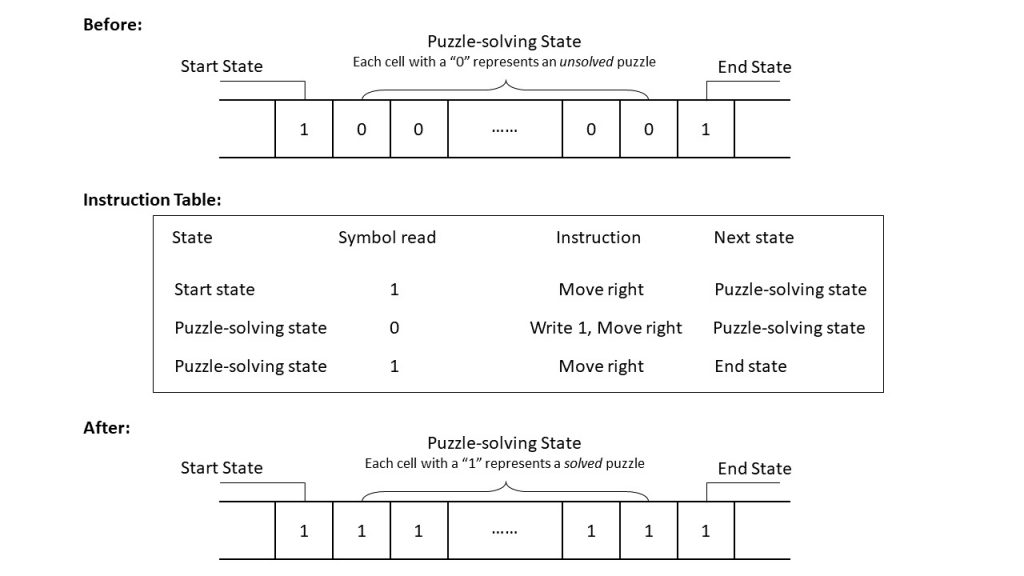
Figure 3. The puzzle-solving process in escape rooms can be modeled as a Turing Machine.
Before the game, the tape has a cell with “1” denoting the start and another denoting the end. In between the two is a series of cells with “0” denoting unsolved puzzles. Players are the header in this Turing Machine. The machine runs with the instructions written in the table. When it is in the start state and the header reads a “1” in the cell, it moves the header to the right and updates the new state of puzzle-solving. When it is in the puzzle-solving state and encounters an unsolved puzzle (a cell with a “0”), it writes a “1” (solve the puzzle) and moves to the next puzzle. The machine stays in the puzzle-solving state and solves puzzle until when it reaches the cell that denotes the end and switches to the stop state.
This is just a simple illustration of a Turing Machine with a program that overwrites 100…001 with 111…111 where “100…001” represents a game with a start “1”, a series of puzzles to solve “00…00,” and an end “1,” and “111…111” represent a finished game with all the puzzles solved. This machine with state updates is also often referred by game developers as a “state machine.”
However, unlike the layout of the cells on the tape in the Turing Machine model, the sequence of puzzles is not necessarily linear. In the following section, I introduce the object graph model that can better visualize the organization of puzzles in escape rooms.
The Object Graph Model
The concept of puzzle path, or puzzle organization, is an under-explored idea in the discourse on escape rooms. Scott Nicholson introduces three basic organizations for puzzles: Open, Sequential, and Path-based.. These three basic paths can form further complicated structures such as a pyramid model. However, the reality is many escape rooms have far more complicated organizations than the basic ones. Escape room designers also use wireframes to design how puzzles are connected and grouped.
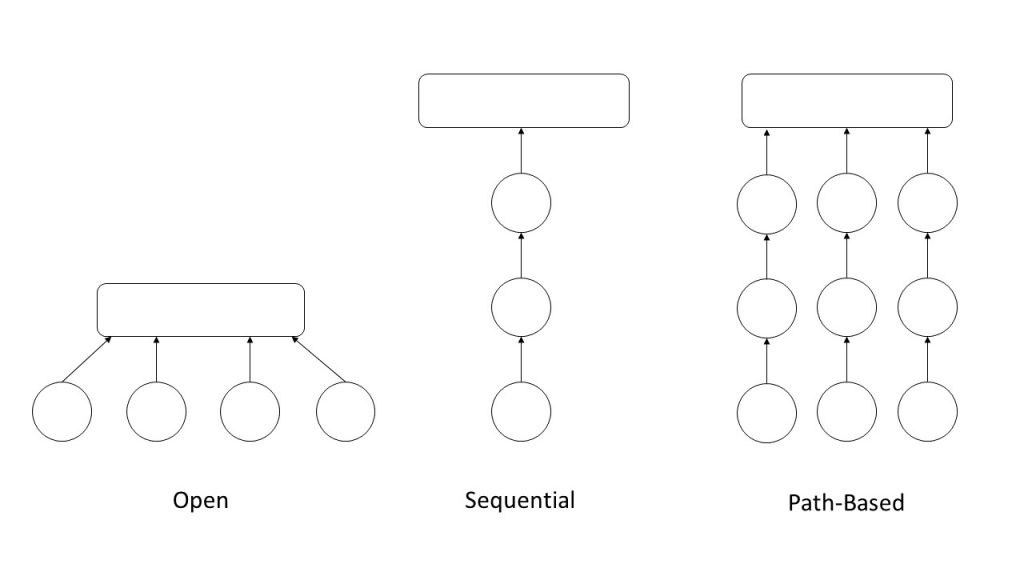
Figure 4a: Three basic organizations for puzzles introduced in Scott Nicholson’s whitepaper.
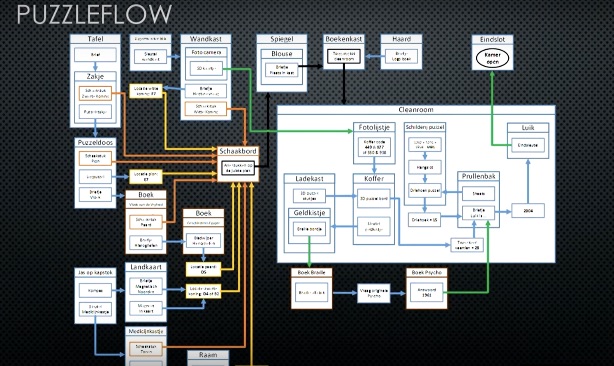
Figure 4b: A complicated wireframe of puzzle flow, presented by escape room designer Thijs Bosschert in his talk “The art of creating an escape room” at Still Hacking Anyway, 2017. Screenshot from https://www.youtube.com/watch?v=0SH0agcMRuA&t=1573s
These two illustrations of puzzle organizations reveal important patterns of puzzle design. First, all the puzzles in an escape room can be expressed by a graph with connected nodes, with each node being an abstraction of an object. Second, basic nodes can be grouped into larger modules, and simple puzzles can form more complex puzzles. As defined by Markus Wiemker, Errol Elumir, and Adam Clare, the term “puzzle” is a challenge that needs to be solved in order to earn the reward. This definition of puzzle reveals important conceptual components of a puzzle, but it does not ground puzzles to objects. For the purpose of establishing a computational model of escape rooms and connecting to the design practice of using object wireframes, I offer an object-oriented model of puzzle design:
All the puzzles in an escape room can be viewed as a graph of connected nodes, with each node being an object in the game. Two nodes are connected if and only if they are part of a puzzle, and the connection describes how the nodes should work with each other to solve the puzzle. A puzzle is a group of connected nodes where one node (puzzle node) takes inputs from other connected nodes (clue nodes).
For example, imagine a simple puzzle that needs to place two statues in two slots on a table in any order. Each of the statues is hidden inside a locked box. The first box has a key lock and the second box has a four-digit lock, and the second box is inside the first box. The key and the four-digit code can be simply found by searching the room. Then the graph should look like the following:
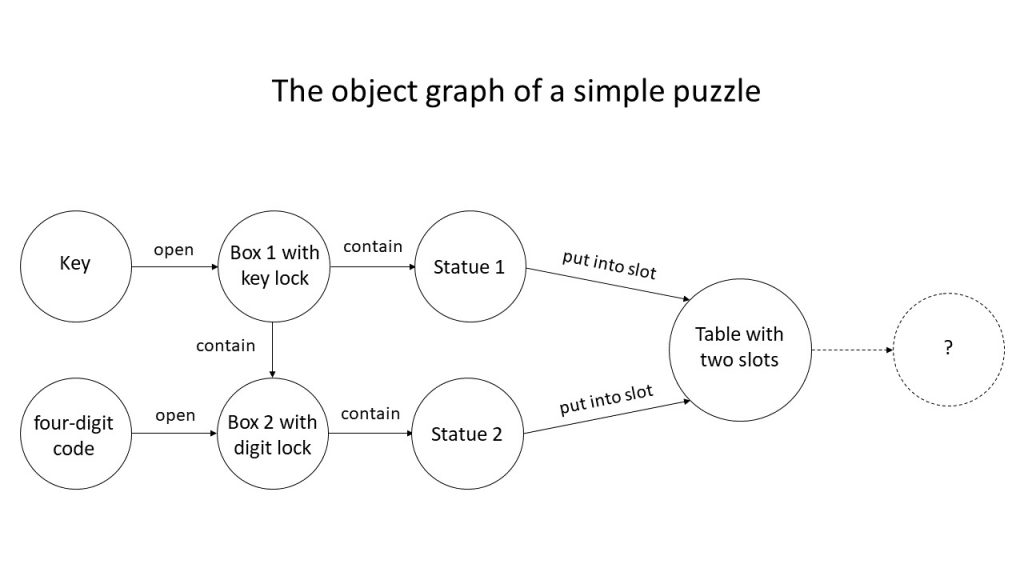
Figure 5. The object graph model. The model here is for a simple system, but in practice the graph will be more detailed.
The object graph demystifies what a puzzle is. It is about the designed interaction and interrelationship between objects that manifest as a challenge to be solved.
Note that puzzles can be hierarchical, meaning that we can view the sub-graph of finding the code to unlock the second box as a puzzle, or the entire graph using all the objects as a puzzle. It is obvious that the above graph will scale into a large network of objects as the number of objects increases. However, what players actually do is always the same – visiting each node in the object graph, until they successfully access the end node, or end when the time runs off. In visualization, the structure of clue nodes connecting to a puzzle node appears the same both in the micro and macro level. This is akin to the beautiful mathematical concept of the fractal in puzzle design.
The object graph provides designers a universal model to design puzzles and the paths to finish the game. It can be used by designers in various ways. For example, designers can use it to dissect what objects are involved and what technology is needed in every puzzle. In doing so, one can manage a bill of materials needed to be purchased and maintained. The graph can also be used to modularize puzzle-solving tasks on an object base. For gamemasters who assist players in the game, they can easily keep a track of players’ process by observing the states of key objects before communicating with players.
It is my intention to use graph, a widely-used data structure in computer science, to emphasize the computational nature of escape rooms. Based on the graph model, we can further discuss running algorithms on the graph and examine the information flow through the paths.
The Computing Model in Players’ Minds: Updating Inventory and Puzzle Lists
Before further discussing the object graph, which is derived from a designer perspective, let us also consider the mental model of players. Most players do not think the same as designers. Players do not keep track of every object along the graph continuum. Even if they track all the objects they have interacted before, they cannot know the objects that are not yet present to them. So, what computational model is it like in the minds of players? How do they perform computing? Because the primary mechanic of the game is puzzle-solving, players are constantly engaged with one or more puzzles. The computing model of players can be expressed with two lists: an inventory list and a puzzle list.
At any time, players as a group have an inventory list of objects found in the room and a list of puzzles to solve. The inventory list contains objects that are clues. Clues are useful to solve puzzles and they are the nodes designers would put on the object graph. However, the inventory list may also contain objects that are purely decorative in the room, or even distracting and misleading to players. When players search the room, they populate the inventory list. At the same time, players may discover puzzles, the objects that need inputs, and add these objects to the puzzle list. When players figure out how to solve the puzzles, they link objects in their inventory list to certain objects in the puzzle list. After a puzzle is solved, the puzzle object may no longer be needed, and it can be removed from the puzzle list. Players get new objects as rewards for solving the puzzle, adding them to the inventory list. Prior objects used to solve the puzzle may be removed from the inventory list if later they are no longer useful to solve new puzzles. Otherwise they may as well be kept in the inventory for solving new puzzles. This process of updating objects in the inventory and puzzle lists loops until the game ends.
The purpose of establishing the two lists is to analyze the order that each node is visited by the players from their perspectives. While the entire graph of connected objects seems too large to be comprehended by players, players actually view it in a flat way and unfolded it step by step. At a time, they only need to think about how to use what they have in the inventory list to solve puzzles in their puzzle list. If they cannot solve it, they may still need to search for objects to add to their inventory list. Therefore, the computational load on the players at a given time in the game is dependent on the number of objects in the two lists at that time.
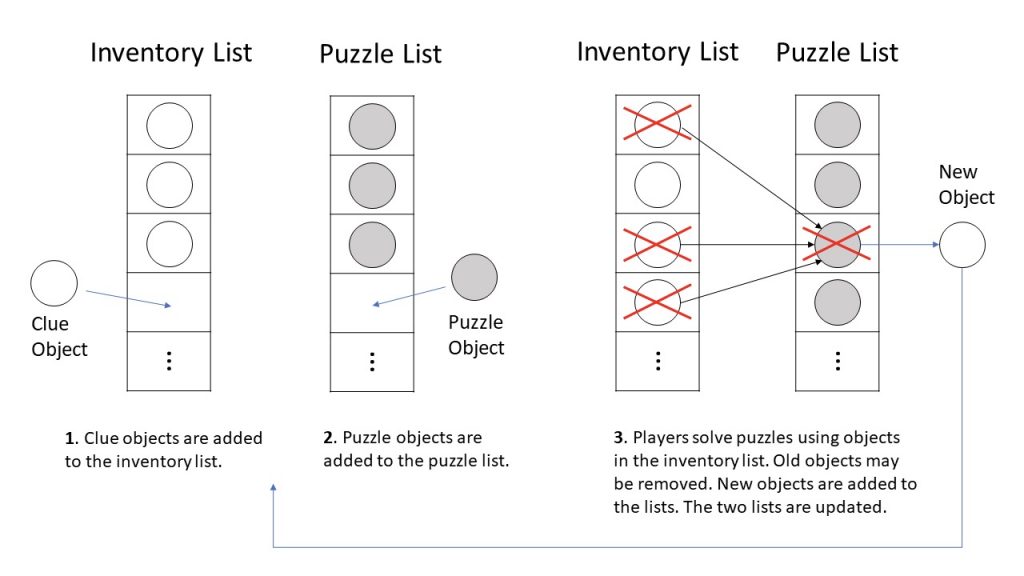
Figure 6. The computing model from the players’ perspective: the loop of updating the inventory list and the puzzle list
An Analog Computing Model Overview.
So far, we have established several foundational computing models to describe the analog computing of escape rooms. Let us now bring the ideas together. Before the game starts, all the objects are reset by a gamemaster to their initial locations and states in the rooms. Using an object graph, designers can visualize the connections between the objects. The following diagram shows an overview of object graph that is also a computing process.
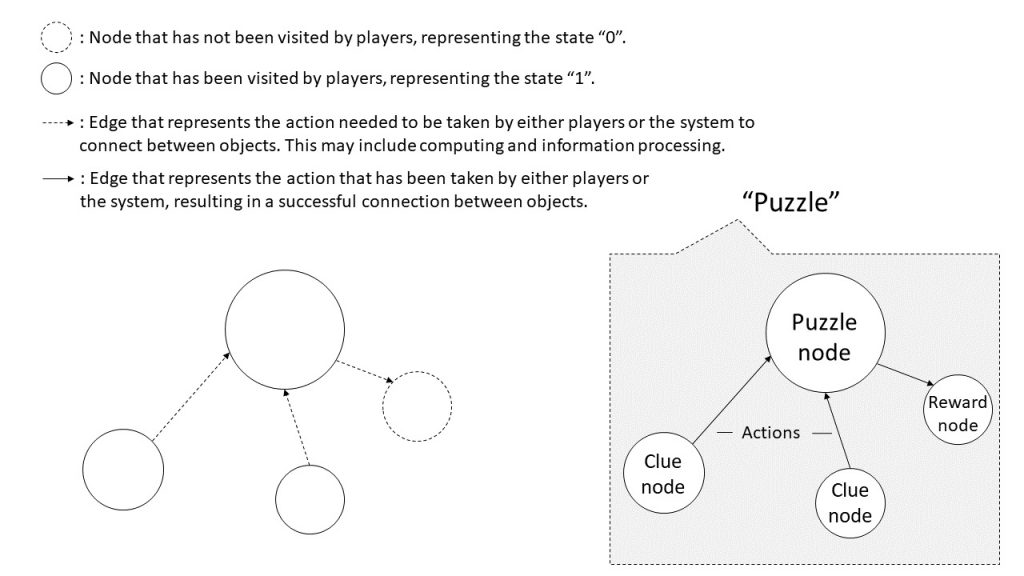
Figure 7. An overview of the object graph model. Left: Players discover objects nodes but have not figured out the connections. Right: The concept of a puzzle is a puzzle node with clue nodes and reward nodes, the connections between nodes are actions taken by players or the system.
Each node in the graph can be visited by players, triggering a 1-bit state change in the game system. Some nodes are puzzle nodes. A puzzle node is an object that needs inputs and forms a challenge to be solved. Puzzle nodes are usually connected with clue nodes and reward nodes. The subgraph of a puzzle node and all its neighbors forms the concept of a puzzle. Once players have visited (“discovered”) all the clue nodes and the puzzle node, they use human power to figure out the connections between all the clue nodes and the puzzle node. The connections (edges) between objects can be automatically triggered by the system through a circuit, but more usually, they demand human actions, for example, figuring out the how one object can function with another, deciphering a code, speculating the relative positions of objects, and manipulating objects. Once all the connections to the puzzle node have been successfully worked out, the puzzle usually leads to the reward of access to new objects in the graph, namely, new nodes being visited. This process keeps going until the end of the game.
It can be tricky when thinking about where “information” fits in the model. Node that the information given to players in any form in the game, such as a code on a piece of paper and a message delivered through a voice recording, is considered as an object in the graph, whereas the information that needs to be processed in players’ minds or by the system are the connections between objects.
A typical conversation between players and the gamemaster of the escape room and shows how the players’ computing model differs from that of the designer. When players get stuck in a puzzle and ask the gamemaster for a hint, the gamemaster needs to check the states of the object graph: which node are the players talking about? Have they discovered all the clue nodes that are supposed to connect to the puzzle node? If so, have they figured out how to connect the two? Based on these states, the gamemaster gives players hints to help them move on. However, the gamemaster may hear a different statement from the players: We have found A, B, and C, and we need to solve X and Y –– how do we do it? This difference reveals mapping between the model from the gamemaster/designer’s perspective and the model from the players’ perspective. Players only see a part of the graph at a time. After searching the room, they collect an inventory list of what they think may be the clue nodes and a puzzle list of what they think may be the puzzle nodes. These two lists are constantly being updated during the game, and it is the process of updating these two lists that unfolds the object graph that the game designers have planned.
Based on the object graph model and our prior discussion on analog computing platforms, we can say that escape room is an analog computing platform involving objects and minds. An escape room game is a puzzle program of visiting and connecting the nodes in the designed object graph. Players are the driving force of the computing. They are like the electric current that activates the static nodes and carries bits of information to flow in the platform. The objects and human power are the hardware layer, and the object graph is the software layer.
Spatial Characteristics of Escape Rooms
As we discussed earlier, the playing-card-as-platform has the following five characteristics of its materials: planar, uniform, ordinal, spatial, and textural. If we consider a card as a 2D object, the 3D objects in escape rooms will hold or extend the characteristics for the 2D objects. For example, a card being planar makes one side of it display information, while another side conceals information. In escape rooms, objects with planar structures provide the same functionality, such as a table, a door, a mat, a curtain. They can hide information behind them. Planarity can even be extended to multi-planarity for a 3D object, with which the information can be displayed and concealed on more than two planes. One application of this is perspective puzzles, where the hidden information is only legible when players view it from a certain perspective.
The spatial characteristics of escape rooms make a significant difference from those of playing cards. Unlike cards of the size of being held and manipulated by hands and thrown on a table, some objects have enough space inside them to accommodate a human body. In an Egypt-themed game, I was put into a coffin; when the cover was closed, I was able to see the fluorescent words on the cover. In an horror-themed game, I stepped into a cabinet; after the door was closed, the whole cabinet started moving. When it stopped and I opened the door again, I was in a new space with only stairs leading to the dark underground. In a prison-themed game, players were separated into three small prisons, each of which had tools that were useful to others but not reachable by others. The bodies of players can also be useful objects to connect objects that are far away from each other. For example, there is a puzzle where four players need to link their hands and arms together to conduct electric current from one object to another.
Besides having big objects as containers to accommodate players, the room itself is a container that contains small objects distributed in it. Unlike cards that are gathered on a table or on a player’s hands, small objects in escape rooms are not initially within reach. They force players to physically and constantly move in the room to carry them from one location to another. In a bunker-themed game, we had to collect electric wires distributed in the first room to plug into holes on an electric box. After we unlocked the second room, we needed to move the electric box with us to solve the puzzles in the second room. In a zodiac-themed game, we needed to keep carrying small sculptures of various constellations during the whole game and use them to collect new sculptures until we had collected all of them. Furthermore, an entire small space inside a big room can be movable. In a game where we were asked to get out of a small room and closed its door, after a minute when we reopened the door, we saw a different room with the scene to represent a different time of the original room. In an Atlantis-themed game, the final room is designed as an escape hatch inside a ship and we needed to push a wall hard to move an exit out.
Looking back to our object graph model, one thing that the spatial characteristics of escape rooms affect in the computing model is the location of players and objects. Location is the new variable brought by the game. Designers can further annotate the location of objects and their distances to one another on the object graph. The distances between objects can be changed in the game at different stages. With the distances counted in the computing model, we can analyze how complex it is to move all the objects. A gamemaster can then kindly inform prospective players about “heavy physical exercise.”
Divide-and-Conquer
With the location being a factor counted in our computing model, we can discuss algorithms and the dynamics of players that are based on locations.
Although players seem to be the driven force of the game, the computing power of players is structured by the platform. There are cases where players are likely or forced to split into subgroups, like circuits divided into parallel connections. First, when players find more than one puzzle (node) at a time, they are likely to divide into sub-groups and work in parallel on each puzzle. In this case, players are divided by the number of puzzles in their list. Second, when one puzzle requires jointed inputs or logic connections of objects that are fixed at remote locations, players are also likely split into sub-groups at remote locations of the objects to exchange their information. Third, players can be forced to split into different spaces by the game rules. For example, players can be blindfolded before entering the room and find themselves at different starting spots where they are blocked from each other. Some games also give players roles and individual paths. Players choose to divide-and-conquer because this strategy allows them to do “parallel computing” and maximizes their efficiency against the time limit in the game. Therefore, the division and gathering of players are foreseeable by looking at the distribution of objects and spaces in escape rooms.
Having more players in the system does not guarantee having more effective power in the game system, however. Some puzzle objects can only be operated by a fixed number of players. Some places can only accommodate a fixed number of players. I was in a seven-player game where the last puzzle of the first room is in a very small space. Three of us were crouched around a small TNT control device that needed to be activated in order to bomb the door open. It was a complicated puzzle that required a lot of mental labor. All the instructions and clues were on a small piece of paper. However, the rest of us four could not even see what was written on the paper because our sight was body blocked. We had nothing to do but stand still in the room waiting for our teammates in front of us to solve the puzzle. At that moment, I felt uninterested and useless to make any progress, such as when programs on my desktop computer stop responding.
Conclusion and Discussions
The main contribution of this paper is a formal analysis of escape rooms as an analog computing platform. It proposes two major computing models of escape rooms: the object graph model and the player model that matches inventory lists to puzzle lists. Unlike digital computing systems, escape rooms reconfigure the relationship between humans and objects in computing. As the object graph model shows, the puzzle-solving process is by nature a Turing Machine, but also involves human power to update its states. Players perform the computing inside rooms of objects by updating an inventory list and a puzzle list. Their group dynamics are structured by the material and spatial characteristics of the rooms.
The basics of computing in escape rooms continue to reshape platform studies of analog games. Following the momentum of Altice’s work, this study shows how a larger analog game system can be a computer. It identifies basic one-bit processors but also shows that more complicated models of updating graphs and lists can be the essential run-time behaviors of an analog game platform. By highlighting both the role of materiality and the role of human actions in the computing process, this study provides a method for future platform studies to dissect the intertwined relationships between objects and minds through the lens of computing.
As platforms are the bottom level under code, form/function, interface, reception/operation and are situated in culture and context, how will the new focus on the computing under the platform influence these higher levels and the culture? I offer that the study of analog computing may even subvert the traditional hierarchy because the analog computing of the platform involves (instead of underlies) forms/functions and interfaces of objects. These levels are mutually dependent in analog game systems, where forms/functions and interfaces of objects will largely shape the object-object and human-object interactions. Future work can further explore how patterns of forms/functions and interfaces will structure player dynamics and human power in the escape room platform.
From a designer’s prospective, I hope that the object-based models proposed in this paper will help facilitate the design and development of escape rooms. The computing models may be a useful template to design storytelling in escape rooms. Escape rooms have evolved to have characters, narrative, scenic design, live actors, and even replayable content. Scott Nicholson emphasizes that storytelling should be connected with puzzles. The object-based models can offer a practical strategy for designing consistency between puzzles and storytelling. While the entire game is a meta puzzle of puzzles, it can also be a grand narrative threaded by micro-narratives. The process of solving a puzzle resembles the structure of a story: encountering challenges, looking for clues, and overcoming challenges. Viewing the object graph as a story graph, designers can put puzzles and storytelling on the two sizes of an equation for object-based storytelling. If a story is clear to the designers, then they can break the story into small pieces and design each object, connection, and puzzle to bear the same meaning of each story piece.
If we view escape rooms as a platform, can we then invent tools to facilitate the game development process on this platform? Imagine a software interface on which designers can edit an object graph with the ability to add/remove objects, move them around, connect them with lines, and write instructions and stories, etc. The software might automatically deploy programs to the embedded systems in the room, saving labor for fast game design iterations. Before the game is on, gamemasters only need to reset locations of objects and hit one reset button to prepare for the game. When they are asked to provide hints during the game, they simply take a look at the state of the object graph, without the need to ask players where they are in the game. Advanced design systems of escape rooms like this will marry digital computing and analog computing, so that the design space and its community will continue to grow in the future.
––
Ke Jing is a game developer, software engineer, and PhD candidate in the Department of Informatics at the Donald Bren School of Information and Computer Sciences at the University of California-Irvine. His dissertation examines the emerging best-practices of interaction design for Extended Reality (XR) platforms by studying XR games. Ke is one of the developers of the XR Interaction Toolkit for the Unity Engine. He is dedicated to the movement of VR, AR, and hybrid physical-digital games and interaction platforms by empowering content creators with knowledge and tools. Ke likes playing escape rooms, mystery murder games, and MMOs with friends.
––
Featured image by Kdwk Leung on Unsplash

